Poisson MLE via Homomorphic Computation

Introduction

We present a toy example of a homomorphic computation involving maximum likelihood estimation.

Consider the following data motivated by an example from the mle function in the stats4 R package: we wish to estimate \(\lambda\), the Poisson parameter \(\lambda\) for randomly generated count data y below:

library(stats4)
set.seed(17822)
y <- rpois(n = 40, lambda=10)
# Easy one-dimensional MLE:
nLL <- function(lambda) -sum(stats::dpois(y, lambda, log = TRUE))
fit0 <- mle(nLL, start = list(lambda = 5), nobs = NROW(y))

The function nLL is the negative log-likelihood of the data and the function mle computes the maximum likelihood estimate that can be printed out.

summary(fit0)

## Maximum likelihood estimation
## 
## Call:
## mle(minuslogl = nLL, start = list(lambda = 5), nobs = NROW(y))
## 
## Coefficients:
##        Estimate Std. Error
## lambda    9.175  0.4789311
## 
## -2 log L: 199.5328

logLik(fit0)

## 'log Lik.' -99.76641 (df=1)

Distributed Computation

Assume now that the data y is distributed between three sites, none of whom want to share actual data among each other or even with a master computation process. They wish to keep their data secret but are willing, together, to provide the sum of their local negative log-likelihoods. They need to do this in a way so that the master process will not be able to associate the contribution to the likelihood from each site. To simulate this, let’s partition the data y as follows.

y1 <- y[1:20]
y2 <- y[21:27]
y3 <- y[28:40]

The overall likelihood function \(l(\lambda)\) for the entire data is therefore the sum of the likelihoods at each site: \(l(\lambda) = l_1(\lambda)+l_2(\lambda)+l_3(\lambda).\) How can this likelihood be computed while maintaining privacy?

Assuming that every site including the master has access to a homomorphic computation library such as homomorpheR, the likelihood can be computed in a privacy-preserving manner using the following scheme. We use \(E(x)\) and \(D(x)\) to denote the encrypted and decrypted values of \(x\) respectively.

0. Master generates a public/private key pair. Master distributes the public key to all sites. (The private key is not distributed and kept only by the master.)
1. Master generates a random offset \(r\) to obfuscate the intial likelihood.
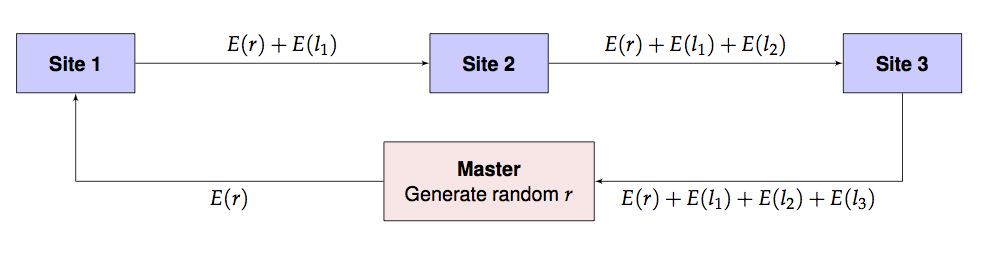
2. Master sends \(E(r)\) and a guess \(\lambda_0\) to site 1. Note that \(\lambda\) is not encrypted.
3. Site 1 computes \(l_1 = l(\lambda_0, y_1)\), the local likelihood for local data \(y_1\) using parameter \(\lambda_0\). It then sends on \(\lambda_0\) and \(E(r) + E(l_1)\) to site 2.
4. Site 2 computes \(l_2 = l(\lambda_0, y_2)\), the local likelihood for local data \(y_2\) using parameter \(\lambda_0\). It then sends on \(\lambda_0\) and \(E(r) + E(l_1) + E(l_2)\) to site 3.
5. Site 3 computes \(l_3 = l(\lambda_0, y_3)\), the local likelihood for local data \(y_3\) using parameter \(\lambda_0\). It then sends on \(E(r) + E(l_1) + E(l_2) + E(l_3)\) back to master.
6. Master retrieves \(E(r) + E(l_1) + E(l_2) + E(l_3)\) which, due to the homomorphism, is exactly \(E(r+l_1+l_2+l_3) = E(r+l).\) So the master computes \(D(E(r+l)) - r\) to obtain the value of the overall likelihood at \(\lambda_0\).
7. Master updates \(\lambda_0\) with a new guess \(\lambda_1\) and repeats steps 1-5. This process is iterated to convergence. For added security, even steps 0-5 can be repeated, at additional computational cost.

This is pictorially shown below.

Implementation

The above implementation assumes that the encryption and decryption can happen with real numbers which is not the actual situation. Instead, we use rational approximations using a large denominator, \(2^{256}\), say. In the future, of course, we need to build an actual library is built with rigorous algorithms guaranteeing precision and overflow/undeflow detection. For now, this is just an ad hoc implementation.

Also, since we are only using homomorphic additive properties, a partial homomorphic scheme such as the Paillier Encryption system will be sufficient for our computations.

We define a class to encapsulate our sites that will compute the Poisson likelihood on site data given a parameter \(\lambda\). Note how the addNLLAndForward method takes care to split the result into an integer and fractional part while performing the arithmetic operations. (The latter is approximated by a rational number.)

library(gmp)
library(homomorpheR)
Site <- R6::R6Class("Site",
                    private = list(
                        ## name of the site
                        name = NA,
                        ## only master has this, NA for workers
                        privkey = NA,
                        ## local data
                        data = NA,
                        ## The next site in the communication: NA for master
                        nextSite = NA,
                        ## is this the master site?
                        iAmMaster = FALSE,
                        ## intermediate result variable
                        intermediateResult = NA
                    ),
                    public = list(
                        ## Common denominator for approximate real arithmetic
                        den = NA,
                        ## The public key; everyone has this
                        pubkey = NA,
                        initialize = function(name, data, den) {
                            private$name <- name
                            private$data <- data
                            self$den <- den
                        },
                        setPublicKey = function(pubkey) {
                            self$pubkey <- pubkey
                        },
                        setPrivateKey = function(privkey) {
                            private$privkey <- privkey
                        },
                        ## Make me master
                        makeMeMaster = function() {
                            private$iAmMaster <- TRUE
                        },
                        ## add neg log lik and forward to next site
                        addNLLAndForward = function(lambda, enc.offset) {
                            if (private$iAmMaster) {
                                ## We are master, so don't forward
                                ## Just store intermediate result and return
                                private$intermediateResult <- enc.offset
                            } else {
                                ## We are workers, so add and forward
                                ## add negative log likelihood and forward result to next site
                                ## Note that offset is encrypted
                                nllValue <- self$nLL(lambda)
                                result.int <- floor(nllValue)
                                result.frac <- nllValue - result.int
                                result.fracnum <- as.bigq(numerator(as.bigq(result.frac) * self$den))
                                pubkey <- self$pubkey
                                enc.result.int <- pubkey$encrypt(result.int)
                                enc.result.fracnum <- pubkey$encrypt(result.fracnum)
                                result <- list(int = pubkey$add(enc.result.int, enc.offset$int),
                                               frac = pubkey$add(enc.result.fracnum, enc.offset$frac))
                                private$nextSite$addNLLAndForward(lambda, enc.offset = result)
                            }
                            ## Return a TRUE result for now.
                            TRUE
                        },
                        ## Set the next site in the communication graph
                        setNextSite = function(nextSite) {
                            private$nextSite <- nextSite
                        },
                        ## The negative log likelihood
                        nLL = function(lambda) {
                            if (private$iAmMaster) {
                                ## We're master, so need to get result from sites
                                ## 1. Generate a random offset and encrypt it
                                pubkey <- self$pubkey
                                offset <- list(int = random.bigz(nBits = 256),
                                               frac = random.bigz(nBits = 256))
                                enc.offset <- list(int = pubkey$encrypt(offset$int),
                                                   frac = pubkey$encrypt(offset$frac))
                                ## 2. Send off to next site
                                throwaway <- private$nextSite$addNLLAndForward(lambda, enc.offset)
                                ## 3. When the call returns, the result will be in
                                ##    the field intermediateResult, so decrypt that.
                                sum <- private$intermediateResult
                                privkey <- private$privkey
                                intResult <- as.double(privkey$decrypt(sum$int) - offset$int)
                                fracResult <- as.double(as.bigq(privkey$decrypt(sum$frac) - offset$frac) / den)
                                intResult + fracResult
                            } else {
                                ## We're worker, so compute local nLL
                                -sum(stats::dpois(private$data, lambda, log = TRUE))
                            }
                        })
                    )

We are now ready to use our sites in the computation.

keys <- PaillierKeyPair$new(1024) ## Generate new public and private key.
den <- gmp::as.bigq(2)^256  #Our denominator for rational approximations

site1 <- Site$new(name = "Site 1", data = y1, den = den)
site2 <- Site$new(name = "Site 2", data = y2, den = den)
site3 <- Site$new(name = "Site 3", data = y3, den = den)

## Master has no data!
master <- Site$new(name = "Master", data = c(), den = den)
master$makeMeMaster()

site1$setPublicKey(keys$pubkey)
site2$setPublicKey(keys$pubkey)
site3$setPublicKey(keys$pubkey)
master$setPublicKey(keys$pubkey)

master$setPrivateKey(keys$getPrivateKey())

master$setNextSite(site1)
site1$setNextSite(site2)
site2$setNextSite(site3)
site3$setNextSite(master)

fit1 <- mle(master$nLL, start = list(lambda = 5))

summary(fit1)

## Maximum likelihood estimation
## 
## Call:
## mle(minuslogl = master$nLL, start = list(lambda = 5))
## 
## Coefficients:
##        Estimate Std. Error
## lambda    9.175  0.4789311
## 
## -2 log L: 199.5328

logLik(fit1)

## 'log Lik.' -99.76641 (df=1)

Applications via distcomp and opencpu

One can imagine these sort of computations being constructed within the framework described the R package distcomp where the sites are opencpu servers and there is a master process executing the computation. Much work remains to be done to make this work in a seamless manner; however, as this proof-of-concept example shows, the technical hurdles are quite surmountable.

CAVEAT

This is an initial proof-of-concept implementation that has to substantially improved for real-world use. You’ve been warned.