Vertically Partitioned Data
Introduction
Li et al. (2016) implement a logistic regression using vertically partitioned data.
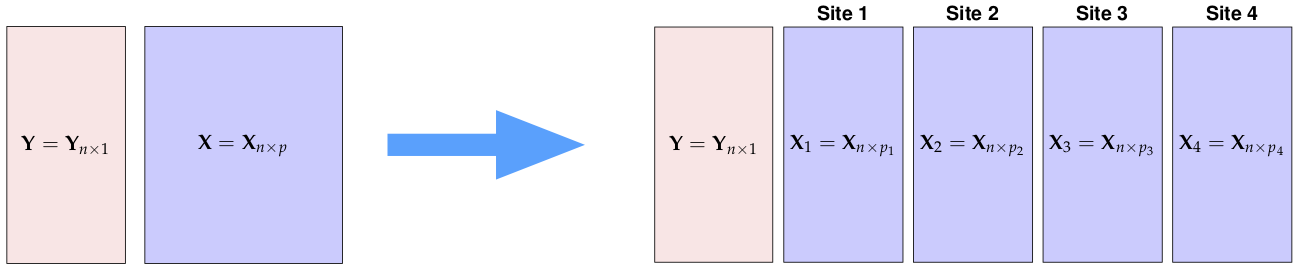
They consider the (ridged) model:
\[ \begin{array}{ll} \underset{\beta}{\mbox{minimize}} & \sum_{i=1}^n \log{(1+exp(-Y_i{\mathbf \beta X_i})} + \frac{\lambda}{2} ||\beta||_2^2. \end{array} \]
To solve this problem in the vertically partitioned setting, they exploit two facts.
- The gram matrix for the global problem is a sum of the gram matrices for each partition:
\[ K = XX^T = \sum_{i=1}^K X_iX_i^T \]
- The dual problem can be formulated, which is:
\[ \begin{array}{ll} \underset{\beta}{\mbox{minimize}} & \frac{1}{2\lambda}\sum_{i,j}\alpha_i \alpha_j Y_i Y_j X_j^T X_i - \sum_{i} L(\alpha_i) \end{array} \] where \(L(\alpha_i) = -\alpha_i\log{\alpha_i} - (1-\alpha_i)\log{(1-\alpha_i)}\).
Note also that:
- There are as many parameters (\(\alpha_i\)) in the dual as observations.
- The \(Y\) is shared among sites.
Implementation
We first generate some synthetic data where we have 1000 observations and 20 parameters.
p <- 10
n <- 100
sigma <- 3
DENSITY <- 0.2
set.seed(18321)
beta_true <- stats::rnorm(p)
X <- matrix(stats::rnorm(n*p, 0, 5), nrow = n, ncol = p)
y <- sign(X %*% beta_true + stats::rnorm(n, 0, sigma))
Y <- (y+1)/2 ## on 0, 1 scale.The Primal Problem
We shall use a parameter \(\lambda = 5\) for concreteness. The problem can be stated directly using CVXR.
suppressMessages(suppressWarnings(library(CVXR)))
beta <- Variable(p)
lambda <- 5
loss <- sum_entries(logistic(-mul_elemwise(y, X %*% beta))) + lambda/2 * sum_squares(beta)
primal_problem <- Problem(Minimize(loss))
primal_result <- solve(primal_problem)
beta_primal <- primal_result$getValue(beta)
print(beta_primal)## [,1]
## [1,] 0.4405501
## [2,] 0.4567835
## [3,] -0.1042528
## [4,] -0.1972774
## [5,] -0.5927040
## [6,] -0.4398515
## [7,] -0.3880561
## [8,] -0.4661118
## [9,] -0.7004535
## [10,] -0.1017521The Dual Problem
We first check that the dual solves the same problem. Here is the dual, once again stated directly in CVXR.
n <- length(y)
alpha <- Variable(n)
XX <- as.numeric(y) * X
tXX <- t(XX)
K <- XX %*% tXX
obj <- 0.5 * quad_form(alpha, K) / lambda - sum(entr(alpha) + entr(1-alpha))
dual_problem <- Problem(Minimize(obj))
dual_result <- solve(dual_problem)
alphaValue <- dual_result$getValue(alpha)
beta_dual <- tXX %*% alphaValue / lambda
print(cbind(beta_primal, beta_dual))## [,1] [,2]
## [1,] 0.4405501 0.4405501
## [2,] 0.4567835 0.4567835
## [3,] -0.1042528 -0.1042528
## [4,] -0.1972774 -0.1972774
## [5,] -0.5927040 -0.5927040
## [6,] -0.4398515 -0.4398515
## [7,] -0.3880561 -0.3880561
## [8,] -0.4661118 -0.4661119
## [9,] -0.7004535 -0.7004535
## [10,] -0.1017521 -0.1017521They should match.
The Dual Problem using Partitioned Data
Here the data is vertically split.
splits <- list(1:3, 4:6, 7:10)
Xs <- lapply(splits, function(ind) X[, ind])
n <- length(y)
alpha <- Variable(n)
## Form XX and its transpose
XXs <- lapply(Xs, function(x) {
XX <- as.numeric(y) * x
tXX <- t(XX)
list(XX, tXX)
})
## The Aggregation Step
K <- Reduce("+", lapply(XXs, function(l) l[[1L]] %*% l[[2L]]))
obj <- 0.5 * quad_form(alpha, K) / lambda - sum(entr(alpha) + entr(1-alpha))
dual_partitioned_problem <- Problem(Minimize(obj))
dual_partitioned_result <- solve(dual_partitioned_problem)
alphaValue <- dual_partitioned_result$getValue(alpha)
tXX <- do.call(rbind, lapply(XXs, function(x) x[[2]]))
beta_dual_partitioned <- tXX %*% alphaValue / lambda
print(cbind(beta_dual, beta_dual_partitioned))## [,1] [,2]
## [1,] 0.4405501 0.4405501
## [2,] 0.4567835 0.4567835
## [3,] -0.1042528 -0.1042528
## [4,] -0.1972774 -0.1972774
## [5,] -0.5927040 -0.5927040
## [6,] -0.4398515 -0.4398515
## [7,] -0.3880561 -0.3880561
## [8,] -0.4661119 -0.4661119
## [9,] -0.7004535 -0.7004535
## [10,] -0.1017521 -0.1017521That also matches.
References
Li, Yong, Xiaoqian Jiang, Shuang Wang, Hongkai Xiong, and Lucila Ohno-Machado. 2016. “VERTIcal Grid lOgistic Regression (Vertigo).” Journal of the American Medical Informatics Association 23 (3):570–79. https://doi.org/10.1093/jamia/ocv146.